二叉树节点结构

1
2
3
4
5
6
7
8
public class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x){
        this.val = x;
    }
}

前序遍历

前序遍历：根结点 —> 左子树 —> 右子树 （根节点在 前中后 那个位置 就叫什么遍历）

img

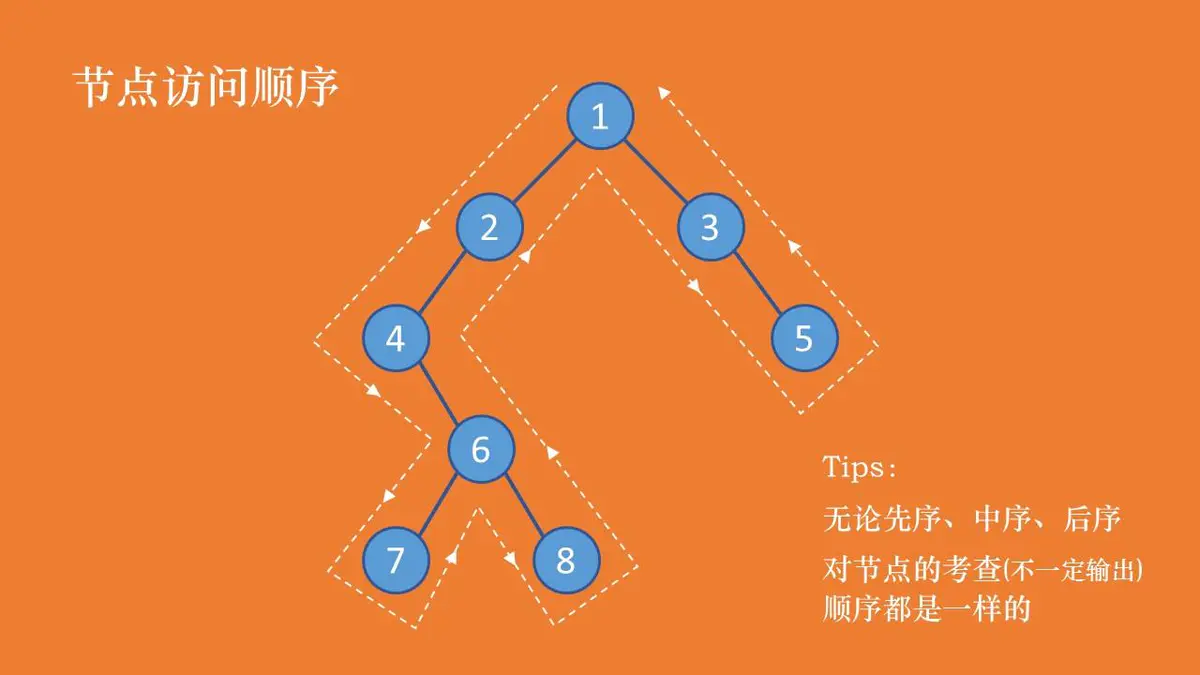
前序遍历：1 2 4 6 7 8 3 5

题目

144.二叉树的前序遍历

递归算法

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    List<Integer> res = new ArrayList<Integer>();
    public List<Integer> preorderTraversal(TreeNode root){
        if (root == null) return res;
        res.add(root.val);
        //一共到达三次root的节点
        preorderTraversal(root.left);
        //返回root
        preorderTraversal(root.right);
        //返回root
    }
    return res;
}

迭代法

img

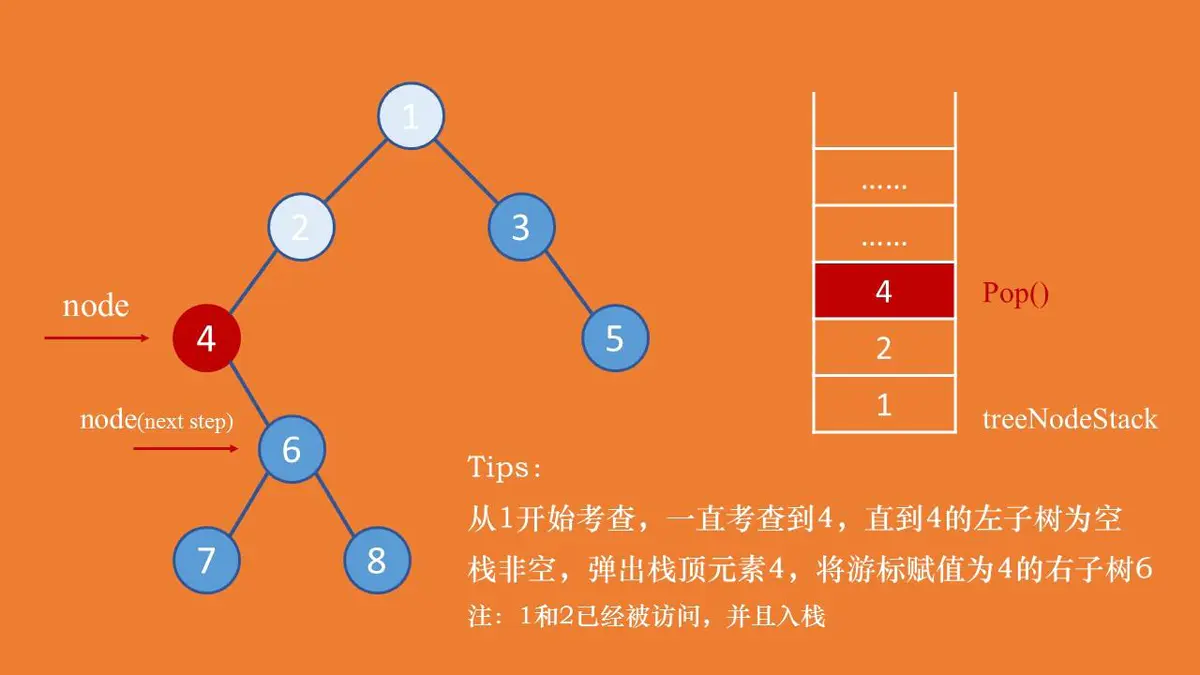
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    //迭代
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while(root!=null || !stack.empty()){
            while(root!=null){
                res.add(root.val); //先将节点加入结果队列
                stack.push(root);  //不断将该节点左子树入栈
                root = root.left;
            }
            root = stack.pop(); //栈顶节点出栈
            root = root.right; //转向该节点右子树的左子树（下一个循环）
        }
        return res; 
    }
    
}

中序遍历

中序遍历：左子树—> 根结点 —> 右子树 （根节点在 前中后 那个位置 就叫什么遍历）

img

中序遍历 ：4 7 6 8 2 1 3 5

题目

94.二叉树的中序遍历

递归算法

1
2
3
4
5
6
7
8
9
10
class Solution {
    List<Integer> res = new ArrayList<Integer>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root == null) return res;
        inorderTraversal(root.left);
        res.add(root.val);
        inorderTraversal(root.right);
        return res;
    }
}

迭代法

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    //迭代
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while(root!=null || !stack.empty()){
            while(root!=null){
                stack.push(root);  //不断将该节点左子树入栈
                root = root.left;
            }
            root = stack.pop(); //栈顶节点出栈
            res.add(root.val); //将节点加入结果队列
            root = root.right; //转向该节点右子树的左子树（下一个循环）
        }
        return res; 
    } 
}

后续遍历

后序遍历： 左子树 —> 右子树 —>根结点 （根节点在 前中后 那个位置 就叫什么遍历）

img

后序遍历：7 8 6 4 2 5 3 1

题目

145.二叉树的后序遍历

递归算法

后序遍历：左子树 —> 右子树 —> 根结点（根节点在 前中后 那个位置 就叫什么遍历）

1
2
3
4
5
6
7
8
9
10
class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) return res;
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        res.add(root.val);
        return res;
    }
}

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null; //pre节点用于记录前一次访问的节点
        while(root!=null || !stack.empty()){
            while(root!=null){
                stack.push(root); //不断将左节点压栈
                root = root.left; 
            }
            root = stack.peek();
            if(root.right==null || root.right==pre){ //若右节点为空 或右节点访问过
                res.add(root.val); //此时可以访问根结点啦
                pre = root;
                stack.pop();
                root = null; //此时下一轮循环不要将左子树压栈，直接判断栈顶元素
            }else{
                root = root.right; //先不出栈 把它右节点入栈
            } 
        }
        return res; 
    }
}

第二种解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//第二种写法
//修改前序遍历代码中，节点写入结果链表的代码：将插入队尾修改为插入队首
//修改前序遍历代码中，每次先查看左节点再查看右节点的逻辑：变为先查看右节点再查看左节点
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        LinkedList res = new LinkedList();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        while(root!=null || !stack.empty()){
            while(root!=null){
                res.addFirst(root.val); //插入队首
                stack.push(root);
                root = root.right; //先右后左
            }
            root = stack.pop();
            root = root.left;
        }
        return res; 
    }
}